Jass Agent using Monte Carlo Tree Search

As a requirement to attend the final exam for this module, we implemented a Jass-playing agent that competed against agents developed by other students. In addition to the implementation, we were required to submit a short technical report and a video explaining our approach and design choices. The agent was developed collaboratively together with Dan Livingston. All figures were originally only used for debugging. The source code can be found on GitHub.

Abstract

This project presents an exploration of artificial intelligence techniques for automating gameplay in Jass, a popular Swiss card game. We implemented bots with various strategies to evaluate performance in both choosing the trump suit and playing cards. Key contributions include the use of rule-based strategies, statistical models, and deep neural networks to optimize gameplay decisions.

Introduction

This work was created for the Deep Learning for Games course at the Lucerne University of Applied Sciences and Arts. We had to implement a bot that plays Jass, a traditional card game widely played in Switzerland.

Methods to Implement

In this simulation of Jass, the bots have to implement two methods. Both methods need to provide a response within 10 seconds or a random move will be played. choose_card, called when the bot has to choose a card to play and choose_trump, called when the bot has to choose the trump.

Information Provided to the Bot

The bot receives an observation of the game containing the information below

• Dealer
• Trump declarer
• Chosen trump
• Whether trump was declared forehand
• Played tricks so far
• Winner and starting player of each trick
• Team points (current round)
• Opponent team points (current round)
• Cards played in the current trick
• Current player
• Player hand

Design Choices

To explore various approaches, strategies were developed for both methods, enabling the testing of different combinations of TrumpStrategies and PlayStrategies. Additionally, PlayRuleStrategies were incorporated, which are evaluated in sequence before triggering a PlayStrategy.

TrumpStrategies

A TrumpStrategy processes an observation of a game to determine a trump suit, selecting from DIAMONDS, HEARTS, SPADES, CLUBS, OBE_ABE, UNE_UFE, or choosing PUSH, which allows the partner to decide the trump suit.

PlayStrategies

It processes an observation of a game and selects a card from the player’s hand to play.

PlayRuleStrategies

This is a list of rules that will trigger before a PlayStrategy is called. This is in order to play no-brainer moves. The strategy will go through the list, and if one is triggered, it will play the card. If no rule is triggered, the PlayStrategy will be called.

Implementations

TrumpStrategies

Five different TrumpStrategies were implemented:

• RandomTrumpStrategy: Chooses a random trump. This strategy cannot choose PUSH.
• HighestSumTrumpStrategy: Selects the trump with the most cards of the same suit. This strategy will not choose OBE_ABE or UNE_UFE and cannot choose PUSH.
• HighestScoreTrumpStrategy: Calculates a score for each trump and selects one if it surpasses a defined threshold. This method was proposed by Daniel Graf in his matura work.
• StatisticalTrumpStrategy: Adopts a statistical approach to choose the trump based on a dataset of 1.8 million games played on swisslos. It evaluates how often a card appeared in the player’s hand when a trump was chosen.
• DeepNNTrumpStrategy: Trained on synthetic data by generating approximately 2’000’000 hands and simulating 20 games for each trump using a random PlayStrategy, resulting in 120’000’000 total games. A neural network was then trained to predict the average points for a given hand, and the trump with the highest predicted score was selected. If the score was below a threshold, the strategy decides to PUSH.

PlayStrategies

• RandomPlayStrategy: Chooses a random valid card from the hand.
• HighestValuePlayStrategy: Chooses the highest value card from the hand.
• MCTSPlayStrategy: Randomly distributes other cards among the players. Then uses Monte Carlo Tree Search to find the best card to play for this hand.
• DeterminizedMCTSPlayStrategy: Takes $d$ random samples of the remaining cards and uses Monte Carlo Tree Search to find the best card to play for this hand. Takes the card that works best on average.

PlayRuleStrategies

• OnlyValidPlayRule: If only one card is valid, play it. This is to save time and resources.
• SmearPlayRule: Smearing is a strategy in Jass where you play a high-value card when the trick is already won.
• TrumpJackPlayRule: If the player has Trump Jack, play it if an opponent played the Trump 9 or the total points of the trick are above 20.
• PullTrumpPlayRule: As long as the opponents have trump cards, play the highest trump card.
• MiniMaxPlayRule: At a certain threshold, switch to the mini-max strategy.
• SwisslosOpeningPlayRule: This was an attempt to code all opening rules from swisslos. We discontinued this because it was too complex and not worth the effort.

Evaluation

The setup involves initializing an Arena. Upon execution, four bots are generated and evenly distributed into two teams. During the course of the games, their positions are adjusted by resetting the Arena halfway through, allowing for a balanced and comprehensive evaluation of performance. We fixed the seed for all experiments and executed them on the same hardware. The results table contain the Winrate and Average Points for both Overall (O) and for only Trump Rounds (T).

TrumpStrategy Evaluation

To evaluate the TrumpStrategies independent of the PlayStrategy, we ran every TrumpStrategy together with the RandomPlayStrategy and no PlayRuleStrategies. The opponent played with a random TrumpStrategy. We played 10’000 games in total.

Strategy	Winrate O	Winrate T	Average Points O	Average Points T
Random	50.00	50.00	78.5	78.5
HighestSum	59.15	69.88	85.8071	93.7382
HighestScore	64.11	78.44	89.8663	101.387
Statistical	62.43	75.24	88.2777	98.3564
DeepNN	65.23	81.08	90.6736	103.2246

PlayStrategy Evaluation

Similar to the TrumpStrategies, we evaluated the PlayStrategies independent of the TrumpStrategy. We ran every PlayStrategy together with the best TrumpStrategy, DeepNNTrumpStrategy, for both teams. The amount of games we played varied due to computational limitations. We played 100 games for MCTS and DMCTS The time limit for choosing a card is 5 seconds, half of the time in the official tournament. For DMCTS we chose 31 determinations, due to hardware constraints.

Strategy	Winrate O	Winrate T	Average Points O	Average Points T
Random	50.00	80.74	78.5	102.9398
HighestValue	46.14	79.40	75.6356	104.0712
MCTS ($d=1)$	62.00	98.00	88.9	117.96
DMCTS	64.00	96.00	90.61	117.1

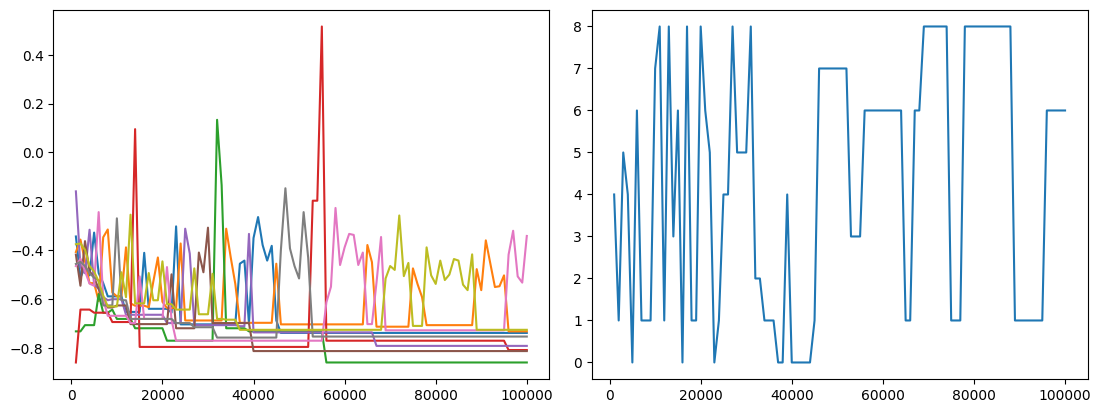
MCTS Iteration–Performance Tradeoff

Further experiments were conducted to identify an optimal number of MCTS iterations. No clear convergence point was observed. For a full hand of nine cards, the search did not converge even after 100 000 node expansions, which is far beyond the maximum number of iterations achievable within the tournament time limit. The identity of the best action continued to change, indicating that no single card consistently dominates. This suggests that the action space cannot be explored sufficiently within a reasonable time budget.

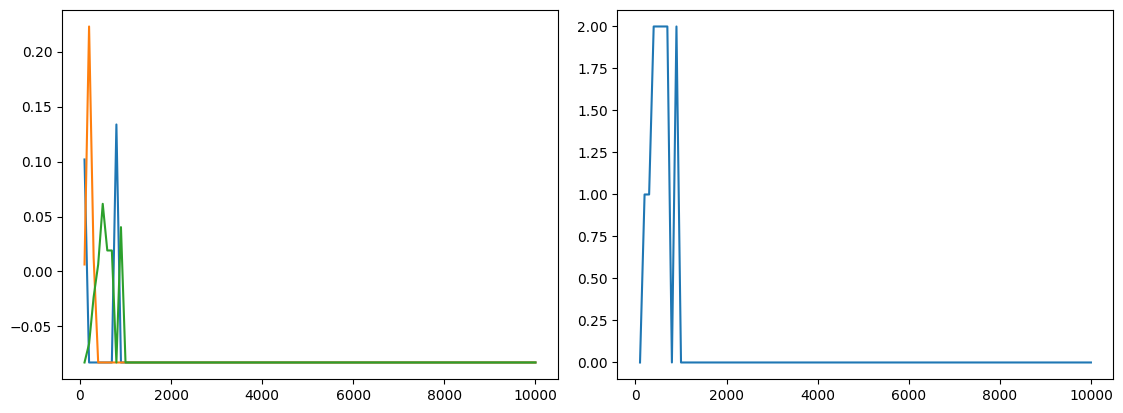
To test whether this behavior is caused by the large action space, the experiment was repeated with only three cards remaining in each hand. Even in this reduced setting, the argmax action continued to change until the search tree was fully expanded.

PlayRuleStrategy Evaluation

For the PlayRuleStrategies, we evaluated them together with DeepNNTrumpStrategy. For the PlayStrategies, we selected RandomPlayStrategy and DeterminizedMCTSPlayStrategy. The amount of games we played varied due to computational limitations. Note that MiniMaxPlayRule was limited to 5 seconds per move and we only ran 100 Games. The runs with DMCTS PlayStrategy were limited to 200 Games

Performance of PlayRuleStrategies for RandomPlayStrategy

Strategy	Winrate O	Winrate T	Average Points O	Average Points T
None	50.00	80.74	78.5	102.9398
OnlyValid	50.00	80.74	78.5	102.9398
Smear	51.08	81.50	79.3933	103.7926
TrumpJack	50.57	81.54	79.2585	104.3382
PullTrump	49.29	80.18	79.0959	104.5728
MiniMax	51.00	84.00	78.46	105.7

Performance of Strategies for Determinized Monte Carlo Tree Search

Strategy	Winrate O	Winrate T	Average Points O	Average Points T
None	48.50	81.00	77.85	103.62
OnlyValid	52.50	88.00	78.745	106.4
Smear	50.50	84.00	78.575	103.07
TrumpJack	52.50	83.00	77.88	103.16
PullTrump	47.50	74.00	77.485	100.78
MiniMax	47.50	79.00	74.82	96.63
All	51.00	83.00	78.79	103.18

Distributed DMCTS Node System

DMCTS is limited by compute power. Because of this, we decided to split the workload across multiple computing nodes. Communication is handled via HTTP. To ensure our response is within the time limit each worker has a separate timeout limit.

Tournament Bot

For the Tournament we combined the DeepNN TrumpStrategy and the DeterminizedMCTS PlayStrategy with the OnlyValid, SmearPlay and TrumpJack PlayRuleStrategies. The final tournament was executed on a distributed cluster consisting of eight devices, with CPU core counts ranging from 2 to 16, resulting in 62 total cores. Empirical experiments showed that the optimal number of determinizations per node is CPU_count − 1. This resulted in a total of 56 determinizations across the cluster.

Results

The tournament consisted of eight matchups, sampled randomly. Each matchup comprised twelve rounds. In every odd-numbered round, the game state was identical (hands and trump caller), while the teams were swapped. Scores were computed by summing all points won per match. The final ranking was obtained by summing scores across all matchups. This evaluation setup favors agents with weaker opponents, as matchups were not skill-balanced.

In the final tournament, we placed 6th out of 16 participants. Four agents were provided by the lecturers as reference points. Two of these placed 1st and 5th, respectively. The 1st-place agent had access to all players cards, giving it a significant advantage. The 5th-place agent used a similar approach to our agent, making it a more meaningful point of comparison. Our direct match against this agent resulted in loss $1060$ to $824$.

Interpretation

Scores overall were plausible. Significant gap in matchup against similar opponent suggest that there is some limitation to our agent. The scores are too close to suggest error with implementation of DMCTS. Our interpretation is that due to the overhead of communicating with 8 different devices the determinizations couldn’t run as many iterations as hoped.